Adjoint bundle
In mathematics, an adjoint bundle [1] [2] is a vector bundle naturally associated to any principal bundle. The fibers of the adjoint bundle carry a Lie algebra structure making the adjoint bundle into an algebra bundle. Adjoint bundles has important applications in the theory of connections as well as in gauge theory.
Contents |
Formal definition
Let G be a Lie group with Lie algebra 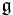 , and let P be a principal G-bundle over a smooth manifold M. Let
, and let P be a principal G-bundle over a smooth manifold M. Let
be the adjoint representation of G. The adjoint bundle of P is the associated bundle
The adjoint bundle is also commonly denoted by 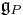 . Explicitly, elements of the adjoint bundle are equivalence classes of pairs [p, x] for p ∈ P and x ∈
. Explicitly, elements of the adjoint bundle are equivalence classes of pairs [p, x] for p ∈ P and x ∈ 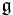 such that
such that
for all g ∈ G. Since the structure group of the adjoint bundle consists of Lie algebra automorphisms, the fibers naturally carry a Lie algebra structure making the adjoint bundle into a bundle of Lie algebras over M.
Properties
Differential forms on M with values in AdP are in one-to-one corresponding with horizontal, G-equivariant Lie algebra-valued forms on P. A prime example is the curvature of any connection on P which may be regarded as a 2-form on M with values in AdP.
The space of sections of the adjoint bundle is naturally an (infinite-dimensional) Lie algebra. It may be regarded as the Lie algebra of the infinite-dimensional Lie group of gauge transformations of P which can be thought of as sections of the bundle P ×Ψ G where Ψ is the action of G on itself by conjugation.
Notes
- ^ J. Janyška (2006). "Higher order Utiyama-like theorem". Reports on Mathematical Physics 58: 93–118. [cf. page 96]
- ^ Kolář, Ivan; Michor, Peter; Slovák, Jan (1993) (PDF), Natural operators in differential geometry, Springer-Verlag, http://www.emis.de/monographs/KSM/kmsbookh.pdf page 161 and page 400
References
- Kobayashi, Shoshichi; Nomizu, Katsumi (1996), Foundations of Differential Geometry, Vol. 1 (New ed.), Wiley-Interscience, ISBN 0471157333
- Kolář, Ivan; Michor, Peter; Slovák, Jan (1993) (PDF), Natural operators in differential geometry, Springer-Verlag, http://www.emis.de/monographs/KSM/kmsbookh.pdf page 161 and page 400
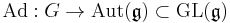
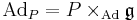
![[p\cdot g,x] = [p,\mathrm{Ad}_{g^{-1}}(x)]](/2012-wikipedia_en_all_nopic_01_2012/I/24e442e37ba0fb1fa4dd55fb79749d1c.png)